레드 블랙 트리의 삭제의 경우 삽입보다 다소 복잡하다고 책에서 말한다. (다소?...)
머리가 나빠 동기들이 많이 도와줬음에도 혼자 이해하는데 2일이 꼬박 걸린 듯하다.
아무튼 내가 이해한 바를 정리해 보려 한다.
삭제의 시간 복잡도
삭제도 삽입과 마찬가지로 O(logN)의 시간 복잡도를 가진다.
RB트리의 삭제
우선 노드의 삭제는 두 가지 방법으로 진행할 수 있다.
1. 삭제하려는 노드가 (Z)라면 Z의 오른쪽의 최솟값을 이동시켜 값을 보완한다.
2. Z의 왼쪽의 최댓값을 Z의 위치로 이동시켜 값을 보완한다.
그 이유는 RB트리 또한 이진트리의 원칙을 기본으로 하기 때문에 삭제되는 노드의 오른쪽(삭제되는 노드보다 큰 값들의 집합)의 가장 왼쪽(최솟값)을 노드로 이동시킨다면 이진트리의 원칙이 깨지지 않고
혹은 삭제하려는 노드의 왼쪽( 삭제되는 노드보다 작은 값들의 집합)중 최댓값을 삭제하려는 노드로 이동시킨다면 이진트리의 원칙이 깨지지 않기 때문이다.
내가 참고한 서적(introduction to algorithms)에서는 1번 방법을 선택해서 진행한다.
사실 삭제되는 노드는 우리가 삭제하려는 노드가 아니다.
우리가 삭제할 노드로 이동되는 원래 노드가 삭제가 된다.
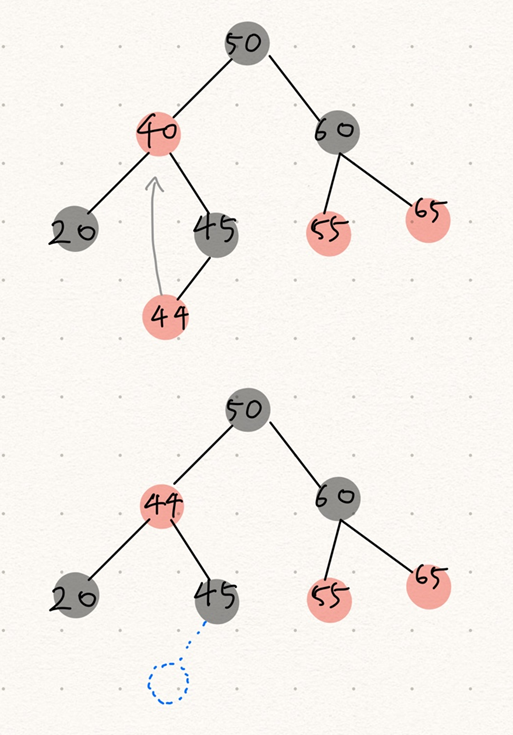
40을 삭제 원한다고 했을 때 실제 삭제되는 노드는 44가 있는 노드이고 44는 40의 위치로 이동한다.
용어 정리
z = (값을) 삭제할 노드 (40)
y = 삭제할 노드를 대체하기 위해 이동하는 노드 (위 이미지에서는 44)
x = y가 이동하며 삭제된 자리를 대체할 노드 (예제 이미지 상에는 없느냐 이동한 y의 자리를 대체할 노드)
w = x의 형제 노드
우리는 노드가 삭제될 때 RB트리의 5번째 특성
루트 노드에서 리프 노드까지 가는 경로상 만나는 검은색 노드의 수는 모두 동일하다
을 생각할 필요가 있다.
만약 실제로 삭제되는 노드(y)의 색이 빨간색이었다면?
빨간색은 자식으로 빨간색을 가질 수 없으며 y로부터 리프노드까지 가는데 필요한 노드의 개수가 N개였다면 y의 자식이 y의 자리를 대체하더라도 특성 5를 유지할 수 있다.
y의 자식은 무조건 검은색이기 때문에 y.p(y의 부모)가 빨간색이었다 해도 특성 4(빨간색 노드의 자식은 검은색이다.)를 만족한다.
(rb트리를 이해할 때 가장 힘들었던 부분이 지금 내가 생각하는 xyzw가 뭐였지 하고 놓쳤던 부분이다. 이 부분을 잘 기억하면서 따라가야 한다.)
따라서 y의 색이 빨간색이라면 그냥 삭제를 진행하면 된다.
실제로 삭제되는 노드(y)가 검은색이라면??
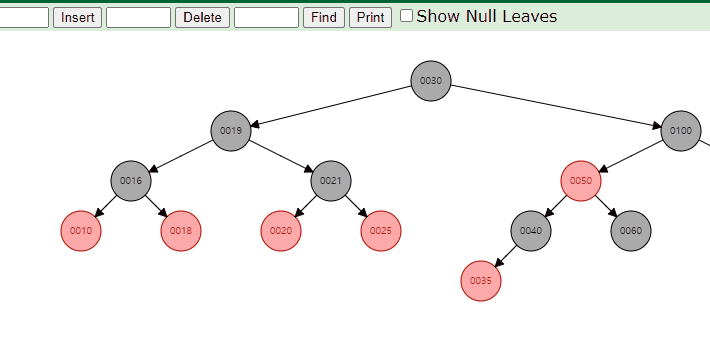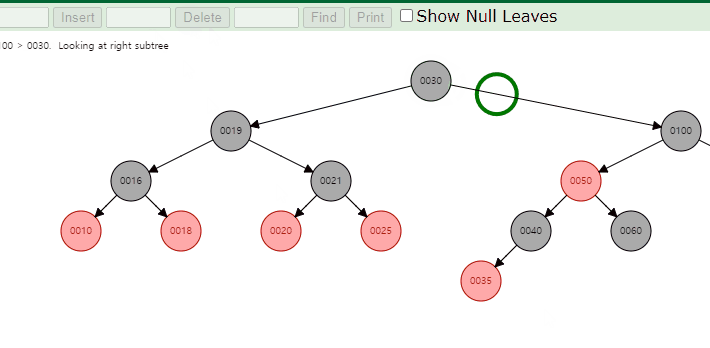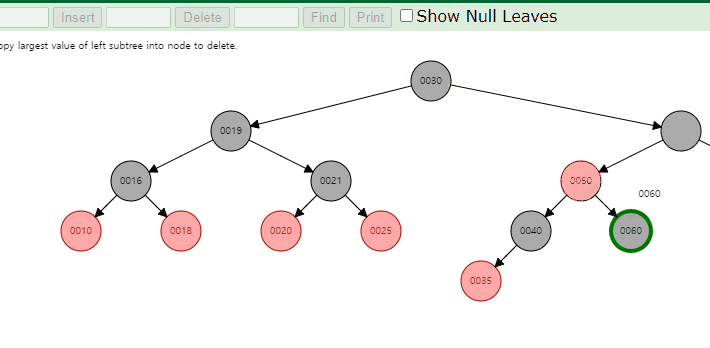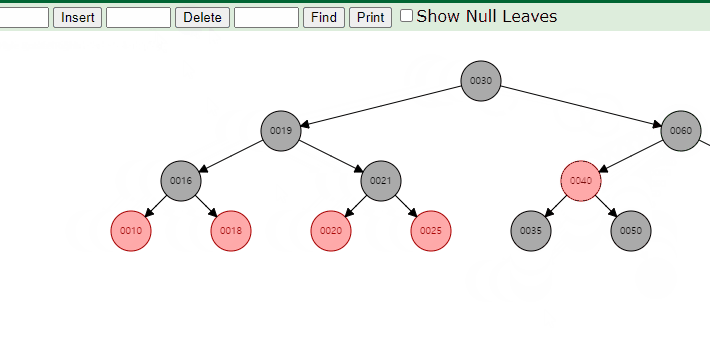
이럴 경우 위와 같이 특성을 만족시켜주기 위해 fixup과정이 필요하다.
위 애니메이션은 left의 max값을 찾아 대체하는 과정이나 검은색 노드가 삭제되었을 때 fixup이 필요한 경우는 동일하므로 참고하면 좋을 것 같다.
그럼 이제 실제 삭제되는 노드(y)가 검은색이었다면 문제가 발생한 다는 사실을 알았다 여기서 이중 흑색 노드 적색과 흑색이 동시에 존재하는 경우 뭐 이런 말이 있다.
호랑이는 죽어서 가죽을 남기는데 노드는 죽어서 색을 남긴다고 생각하자
이는 위의 애니메이션을 보면 null leaf가 진한 흑색으로 생긴다. 이 말은 현재 60이 었던 노드가 지워지지만 그곳에 60의 원래 색(검은색)이 남아있고 null leaf가 검은색이기 때문에 색이 겹쳐 이중 흑색 노드가 되는 거다.
만약 60이 자식을 가지고 있었고 그 색이 검은색이었다면?
마찬가지로 60이 남기고 간 검은색을 자식이 덮으면서 이중 흑색 노드가 되어버린다.
이중 흑색 노드가 뭐길래? 라고 생각할수 있지만 우리는 이때 RB 특성 5를 생각해야 한다.
이중흑색노드가 발생한다는 것의 의미는 흑색이 하나가 줄었다는 것이므로 균형이 깨짐을 의미한다. 그럼 우리의 rb트리는 그 꼴을 못 참기 때문에 어떻게든 회복하려 한다.라고 생각하자
용어 정리 부분에서 우리는 x가 y의 자리를 대체할 노드라고 정의하였다. 따라서 y의 원래 컬러가 black이었고 x의 컬러가 black인 경우 문제가 발생한다.
문제가 발생했을 때 fixup이 필요한 경우를 살펴보자.
경우 1. x의 형제 w가 적색인 경우? ->경우 2,3,4가 될 수 있음
보라색으로 적은 글씨는 각 edge에 연결된 검은색 노드의 수라고 생각하자.
우리는 이 균형을 맞추어야 한다. 위 이미지를 보면 x가 2중 흑색 노드가 되면서 불균형이 발생한다 x.p의 색을 빨간색 w의 색을 검은색으로 변경한 뒤 좌회전시켜주자.
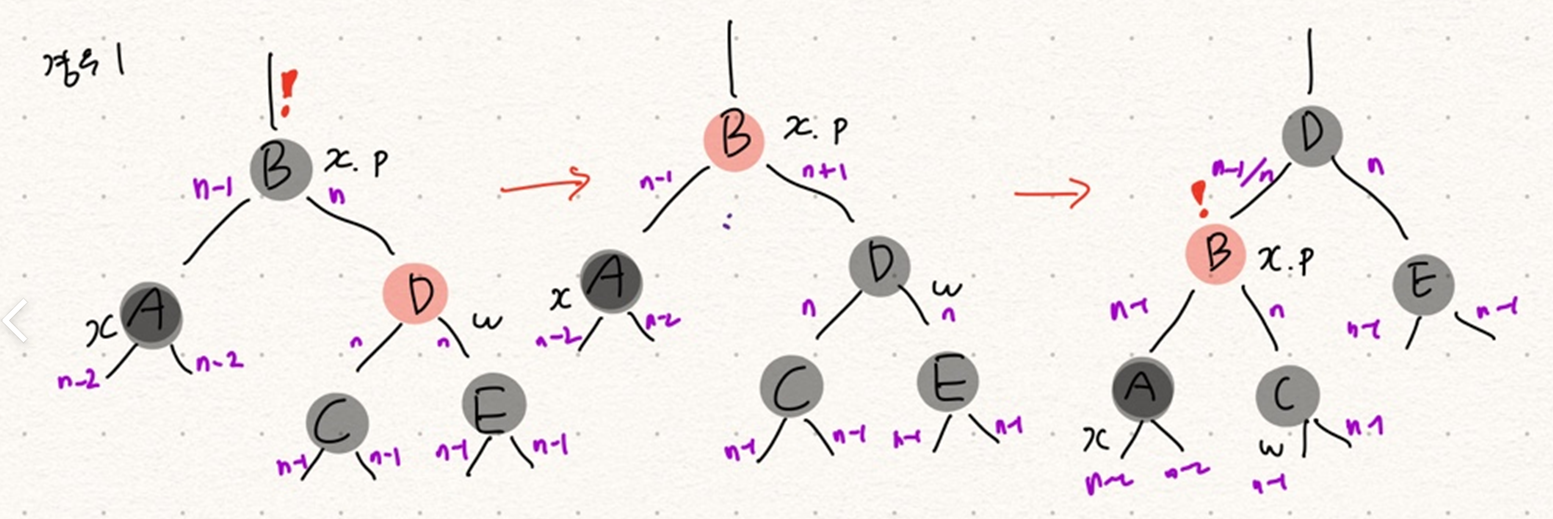
<위 경우를 쉽게 외우자>
자식 중 한 명이 과자를 두 개(이중흑색)먹어 형제가 화가 났다 형제의 싸움을 보고 부모가 화가난다 (화난 형제 진정(검은색))부모가 과자 두개 먹은 자식 놈 혼내려고 내려온다(좌회전)
아직 문제는 해결되지 않았다.
경우 1을 통해 경우 2,3,4 케이스를 고려해야 한다.
경우 2. x의 형제 w는 흑색이고 w의 두 자식이 모두흑색인 경우
경우 3. x의 형제 w는 흑색이고 w의 왼쪽 자식이 적색인 경우
경우 4. x의 형제 w는 흑색이고 w의 오른쪽 자식이 적색인 경우
경우 2. x의 형제 w는 흑색이고 w의 두 자식이 모두 흑색인경우
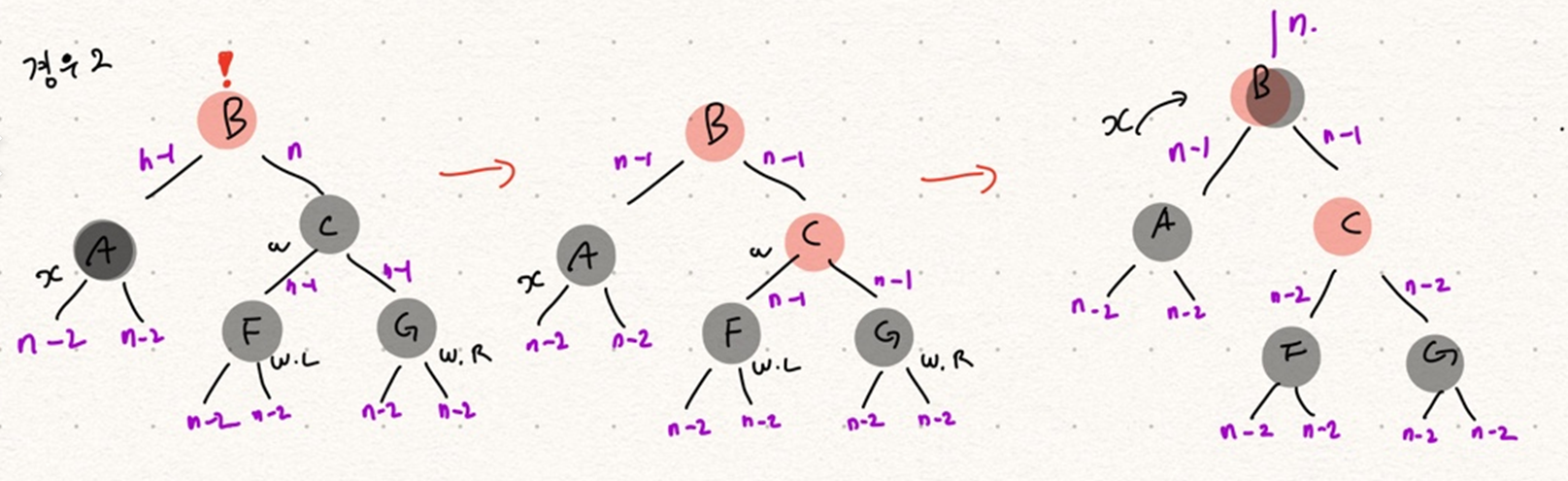
x의 이중 흑색을 벗어나기 위해 x의 형제 w를 적색 노드로 변경함으로써 형제 노드 쪽 흑색 노드의 개수를 줄여준다.
x를 x.p로 하게 되면 x는 순간 부모의 색이었던 적색이 되므로 (x의 컬러가 black인 경우 문제가 발생한다.)는 상황을 벗어난다. 그 이후 x의 컬러를 검은색으로 바꿔주면 모두가 happy 하다.
과자를 두 개 먹어 부모에게 쫓긴 x 새로 만난 형제는 둘 다 착한 (흑색) 자식을 가지고 있다 새로 만난 형제 x의 죄를 자신이 가져간다(빨간색) x는 부모에게 가서 사과한다. 부모의 화가 풀린다 (검은색) happy
경우 3. x의 형제 w는 흑색이고 w의 왼쪽 자식이 적색인경우 -> 경우 4로 연결
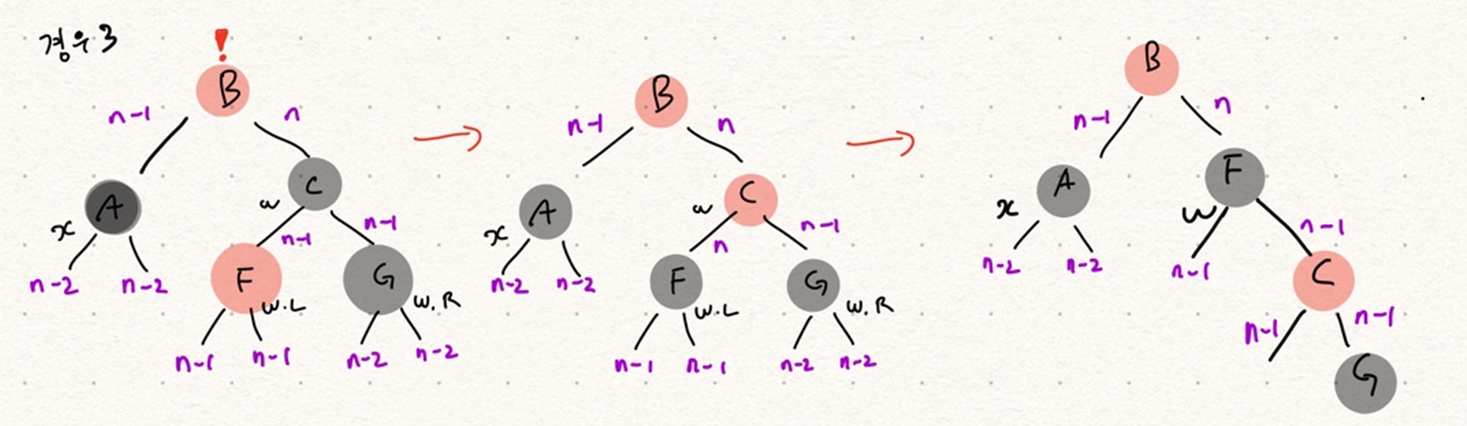
x의 형제 w의 색을 빨간색 w자식의 색을 검은색으로 바꾼 뒤 right 회전시킨다.
경우 1에서 쫓긴 x, 이번에도 w는 착하다 자식의 잘못을 대신 가진다(적색) 그리고 자신의 부모의 눈을 피해 오른 왼쪽 자식의 반대(오른쪽)로 도망간다. x를 쫒던 부모는 감동스러운 w의 행동을 지켜본다. -> 경우 4로 연결
경우 4. x의 형제 w는 흑색이고 w의 오른쪽 자식이 적색인 경우 -> happy
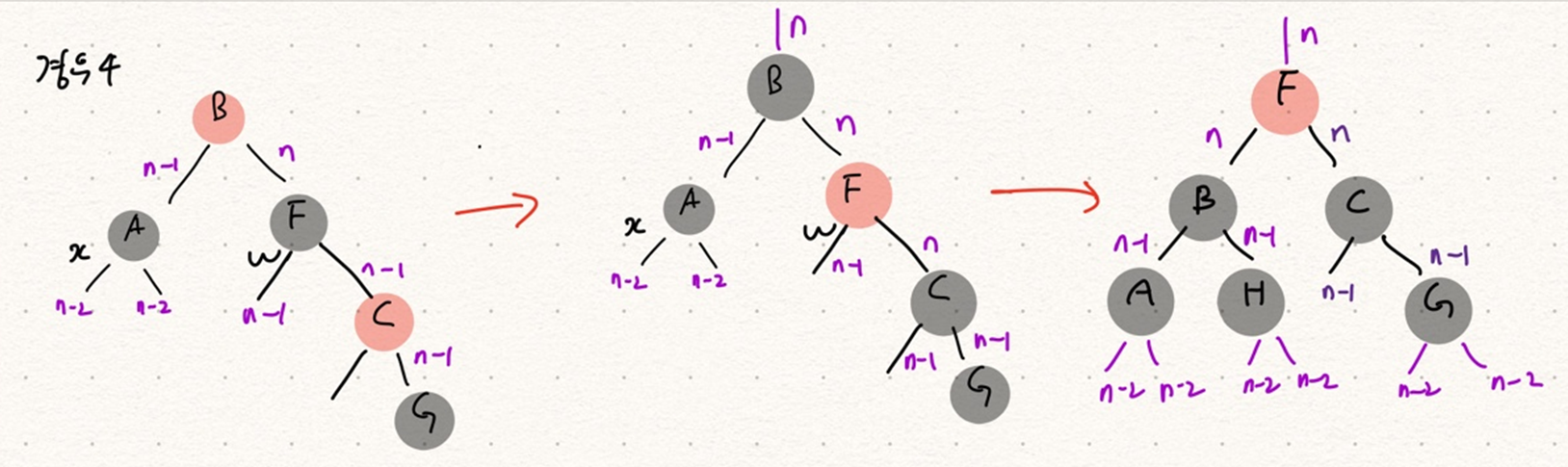
(w는 언제나 x의 형제다.)
x의 형제 w의 오른쪽 자식이 빨간색인 경우 w의 색을 자식의 색과 바꾼다. x.p의 색을 블랙으로 바꾸고 left 회전한다.
경우 4를 만나 fixup 된 경우는 rb트리의 조건을 만족하는 경우로 fixup을 마무리한다.
w는 다시 자식의 죄를 가져와 부모에게 용서를 구한다. 감격스러운 w의 행동을 본 부모는 화가 풀린다(x.p 흑색)
부모는 w가 자기보다 대단하다며 자신의 부모가 돼라 한다. (left 회전) 모두가 해피하다.
x는 어느새 잊혔다...
글이 장황했다
결국 기억할것은 w가 적색인경우 경우 1이 되며 경우 1을 거친이후 경우 2,3,4 가 될 수 있고 흑색이라면 경우 2,3,4 를 돌면서 fixup된다는 것이다.
위의 경우는 x가 left인경우로 했는데 right.이라면? 좌우를 반대로만 해주면 된다.
삭제코드
void transplant(rbtree *t, node_t *u, node_t *v)
{
if (u->parent == t->nil)
{
t->root = v;
}
else if (u == u->parent->right)
{
u->parent->right = v;
}
else
{
u->parent->left = v;
}
v->parent = u->parent;
}
void delete_fixup(rbtree *t, node_t *x)
{
while ((x != t->root) && (x->color == RBTREE_BLACK))
{
if (x == x->parent->left)
{
node_t *w = x->parent->right;
if (w->color == RBTREE_RED)
{
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
w = x->parent->right;
}
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK)
{
w->color = RBTREE_RED;
x = x->parent;
}
else
{
if (w->right->color == RBTREE_BLACK)
{
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotate(t, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
left_rotate(t, x->parent);
x = t->root;
}
}
else
{
node_t *w = x->parent->left;
if (w->color == RBTREE_RED)
{
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
w = x->parent->left;
}
if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK)
{
w->color = RBTREE_RED;
x = x->parent;
}
else
{
if (w->left->color == RBTREE_BLACK)
{
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}
//삭제는 여기서부터
int rbtree_erase(rbtree *t, node_t *p)
{
// TODO: implement erase
node_t *x;
node_t *y = p;
int y_origin_color = y->color;
if (p->left == t->nil)
{
x = p->right;
transplant(t, p, p->right);
}
else if (p->right == t->nil)
{
x = p->left;
transplant(t, p, p->left);
}
else
{
y = node_min(t, p->right);
y_origin_color = y->color;
x = y->right;
if (y->parent == p)
{
x->parent = y;
}
else
{
transplant(t, y, y->right);
y->right = p->right;
y->right->parent = y;
}
transplant(t, p, y);
y->left = p->left;
y->left->parent = y;
y->color = p->color;
}
if (y_origin_color == RBTREE_BLACK) //이중흑색노드 발생
{
delete_fixup(t, x);
}
free(p);
return 0;
}'Algorithms과 자료구조' 카테고리의 다른 글
| 파이썬 알고리즘(소수찾기 에라토스 테네스 체) (0) | 2022.02.06 |
|---|---|
| 해시테이블 (0) | 2022.01.16 |
| RB_Tree(레드블랙트리)_삽입 (0) | 2021.12.05 |

